ビジネスにおいて、施策の効果検証は不可欠です。しかし、データが常に「原因→結果」の順で揃っているとは限りません。本記事では、データが逆の形でしか手に入らない場合に役立つ「ベイズの公式」を使った分析手法を、ビジネスパーソン向けにわかりやすく解説します。サブスクリプションサービスの継続率調査を例に、具体的な計算方法と、ベイズの公式がビジネスやAI分野でどのように活用されているかを紹介します。
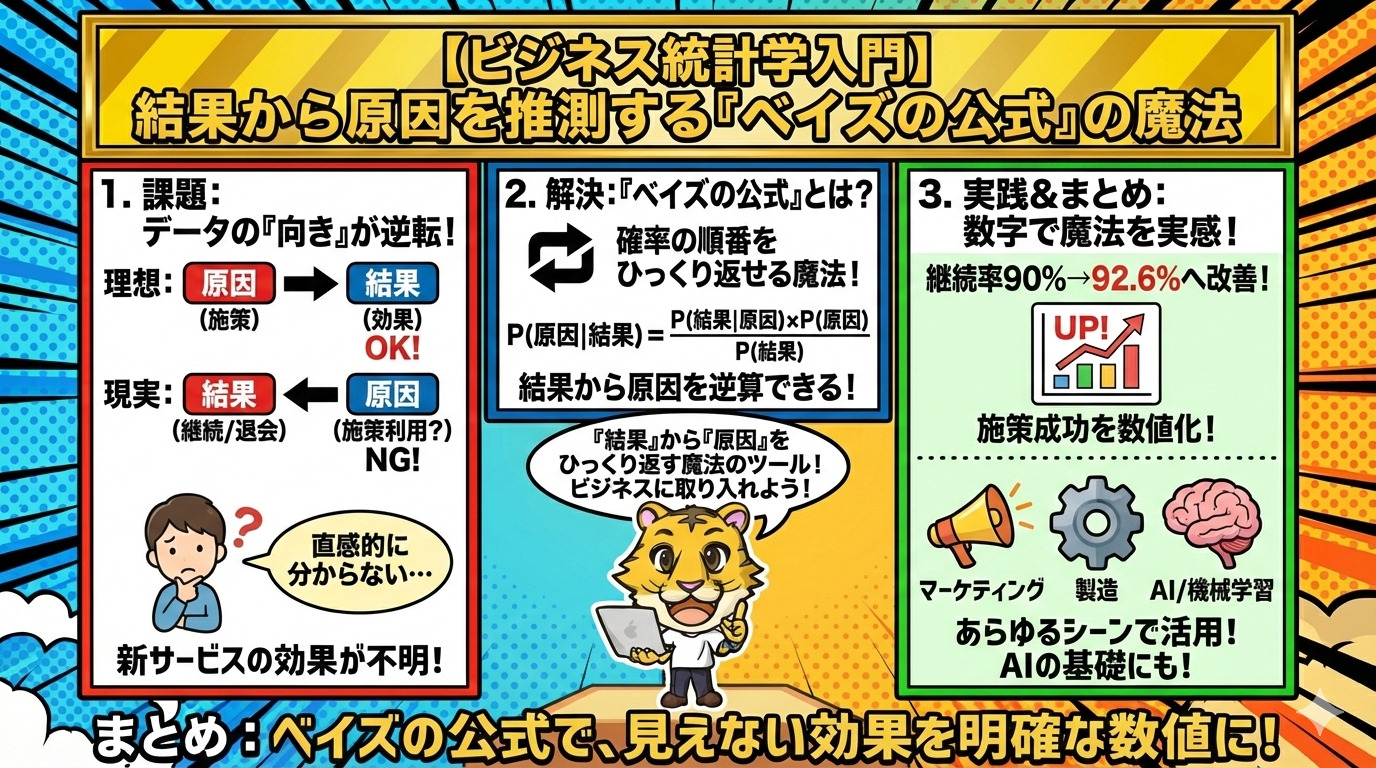
1. データの「向き」が逆転している問題
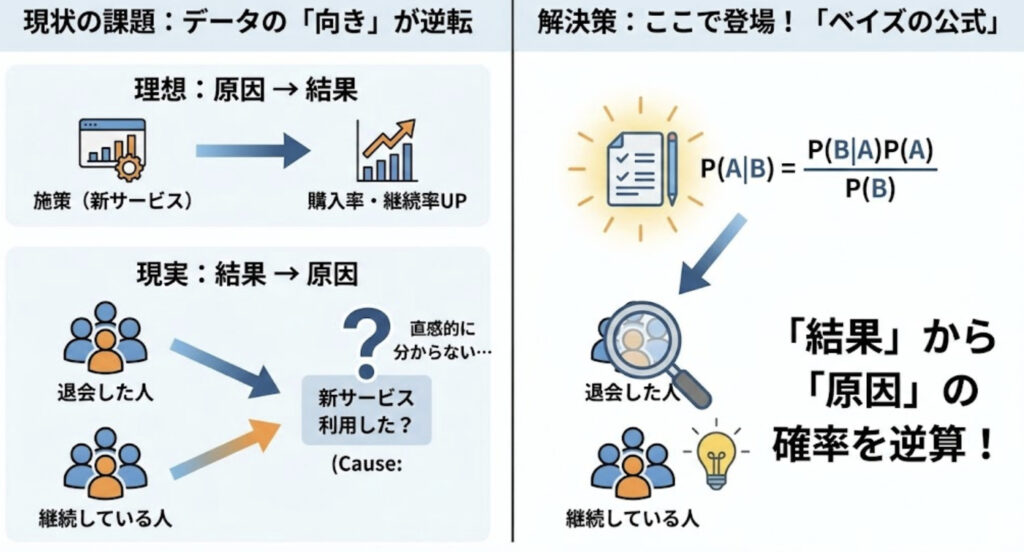
ビジネスにおいて、新しい施策(Web広告の変更、新サービスの導入など)を行った際、その結果として「購入率」や「継続率」がどれくらい改善したのかを検証することは非常に重要です。
通常、Web広告を変更した後に購入率が0.1%から0.15%に上がった、というように「原因(施策)→結果(購入率)」のデータが揃っていれば、分析は非常に簡単です。
しかし、ビジネスの現場では、「結果→原因」の順でデータが得られることが多々あります。
例:サブスクリプションサービスの継続率調査
あるサブスクリプションサービスで、継続率を高めるために「新サービス」を導入したとします。この効果を測定したいときに、以下のようなアンケートデータしか取れないことがあります。
- **退会した人(結果)**に聞いたら:「新サービスを利用しましたか?(原因)」
- **継続している人(結果)**に聞いたら:「新サービスを利用しましたか?(原因)」
このように、「結果(継続or退会)」に応じた「原因(新サービスの利用率)」のデータしか手元にない場合、**「新サービスの利用が、継続率向上にどれだけ寄与したか」**が直感的には分からなくなってしまいます。
ここで登場するのが**「ベイズの公式」**です。
2. ベイズの公式とは?
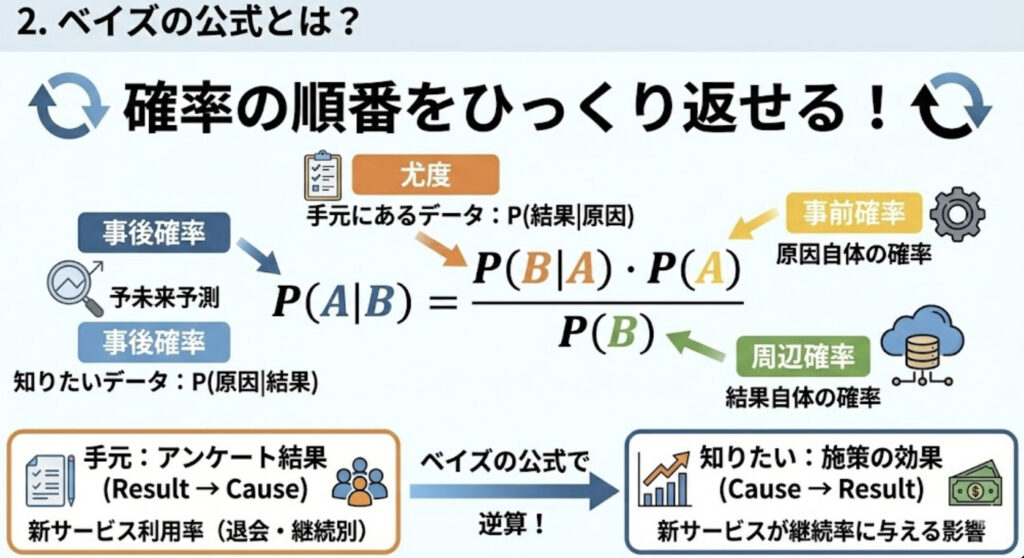
ベイズの公式の凄さは、一言で言うと**「確率の順番をひっくり返せる」**ことです。
- 手元にあるデータ:$P(\text{原因}|\text{結果})$ (結果が出た条件下での、原因の確率)
- 知りたいデータ:$P(\text{結果}|\text{原因})$ (原因が発生した条件下での、結果の確率)
この公式を使えば、手元のアンケート結果(結果→原因)から、本当に知りたい「施策の効果(原因→結果)」を逆算して導き出すことができます。
ベイズの公式は以下のように表されます。
$$
P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}
$$
ここで、
- $P(A|B)$: 事象Bが起きた条件下で事象Aが起きる確率(事後確率)
- $P(B|A)$: 事象Aが起きた条件下で事象Bが起きる確率(尤度)
- $P(A)$: 事象Aが起きる確率(事前確率)
- $P(B)$: 事象Bが起きる確率(周辺確率)
3. 実践!数字で見るベイズの魔法
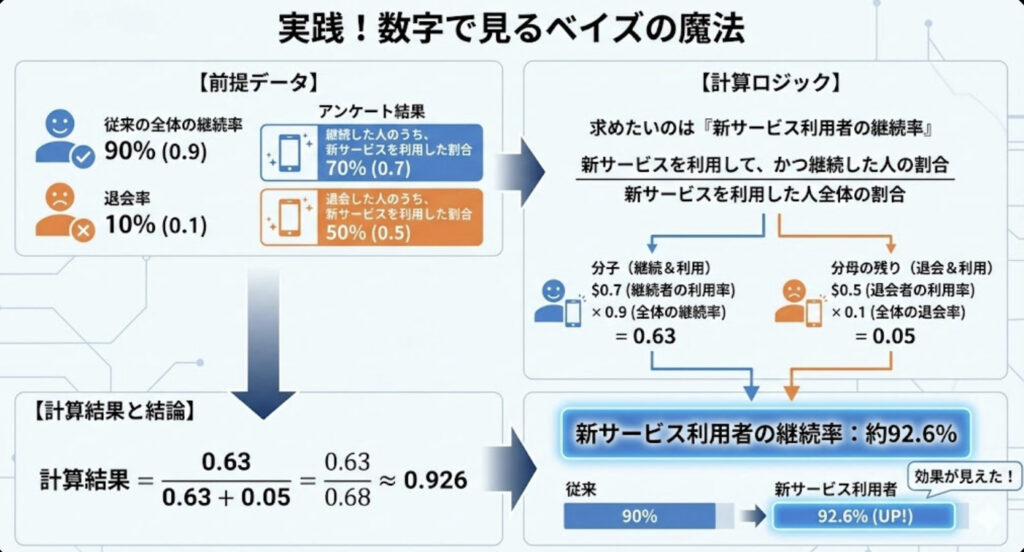
先ほどのサブスクリプションサービスの例で、実際に計算してみましょう。
前提データ
従来の全体の継続率は90%(0.9)とします(つまり、退会率は10%)。
アンケートの結果、以下のデータが得られました。
- 継続した人のうち、新サービスを利用した割合:70%(0.7)
- 退会した人のうち、新サービスを利用した割合:50%(0.5)
これだけ見ても「新サービス利用者の継続率」は分かりません。そこでベイズの公式に当てはめます。
計算ロジック(直感的なイメージ)
求めたいのは「新サービスを利用した人の継続率」です。
$$ \text{新サービス利用者の継続率} = \frac{\text{新サービスを利用して、かつ継続した人の割合}}{\text{新サービスを利用した人全体の割合}} $$
これを手元の数字で計算します。
- 分子(継続&利用): $0.7 (\text{継続者の利用率}) \times 0.9 (\text{全体の継続率}) = 0.63$
- 分母の残り(退会&利用): $0.5 (\text{退会者の利用率}) \times 0.1 (\text{全体の退会率}) = 0.05$
$$ \text{計算結果} = \frac{0.63}{0.63 + 0.05} = \frac{0.63}{0.68} \approx 0.926 $$
ベイズの公式を用いた計算
上記の例をベイズの公式に当てはめてみましょう。
- 事象A: 新サービスを利用する
- 事象B: 継続する
求めたいのは $P(\text{継続}|\text{新サービス利用})$ です。
- $P(\text{継続}|\text{新サービス利用}) = \frac{P(\text{新サービス利用}|\text{継続}) \cdot P(\text{継続})}{P(\text{新サービス利用})}$
ここで、
- $P(\text{新サービス利用}|\text{継続}) = 0.7$ (継続した人のうち、新サービスを利用した割合)
- $P(\text{継続}) = 0.9$ (全体の継続率)
- $P(\text{新サービス利用})$ は、新サービスを利用した人全体の割合なので、 $P(\text{新サービス利用}) = P(\text{新サービス利用}|\text{継続}) \cdot P(\text{継続}) + P(\text{新サービス利用}|\text{退会}) \cdot P(\text{退会}) = 0.7 \cdot 0.9 + 0.5 \cdot 0.1 = 0.63 + 0.05 = 0.68$
したがって、
$P(\text{継続}|\text{新サービス利用}) = \frac{0.7 \cdot 0.9}{0.68} = \frac{0.63}{0.68} \approx 0.926$
結論
計算の結果、**約92.6%**という数字が出ました。
もともとの継続率が90%だったのに対し、新サービスを利用した人の継続率は92.6%に高まっていることが分かりました。つまり、**「この施策によって継続率が2.6%改善した」**と結論づけることができます。
4. まとめ:なぜベイズの公式を学ぶべきか
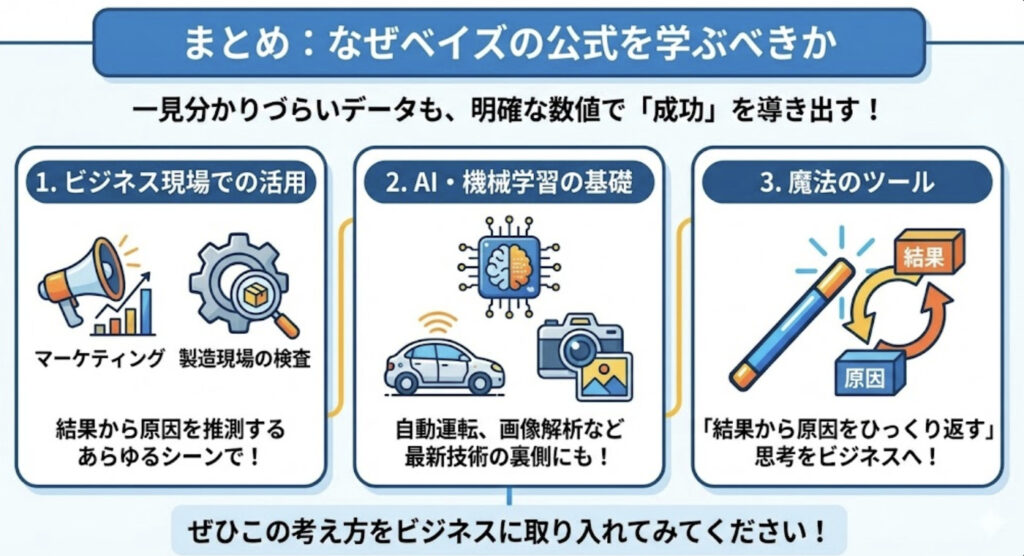
一見すると意味が分かりづらいデータでも、ベイズの公式を使うことで「施策が成功したかどうか」を明確な数値として導き出すことができます。
- ビジネス現場での活用: マーケティング、製造現場の検査など、結果から原因を推測するあらゆるシーンで役立ちます。
- AI・機械学習の基礎: 実は、自動運転、自動翻訳、画像解析といった現代のAI技術の裏側でも、このベイズ統計学(確率的な推論)が使われています。
「結果から原因をひっくり返す魔法のツール」として、ぜひこの考え方をビジネスに取り入れてみてください。




コメント